這篇要記錄邏輯斯迴歸分析(Logistic Regression Analysis),
一種延伸線性迴歸分析(Linear Regression Analysis)的概念,
※※※線性迴歸分析的概念※※※
從我們有興趣的目標群體收集變數, 包含 反應變數(Response Variable)與預測變數(Predictive Variable),
用符號來表示, Y就是反應變數, {X1,...,XP} 就是預測變數. 我們希望了解, Y的數值表現是不是與X有關?
也就是想要知道, 是否存在某一個函數f, 可以把Y與X的關係建立起來:
Y=f(X)
或者更簡單一點說, Y的數值變化是不是能用X的線性組合來描述? 就像是下面所示:
Y=b0+b1*X1+b2*X2+...+bP*XP
上式很清楚表達了, X1變動1個單位, Y會變動 b1個單位. (因為 Y=b1*1, 其他相對而言都是常數, 不會變動)
當然, 這樣的線性組合無法合理解釋真實世界呈現的風貌, 所以 就給他加了隨機誤差在等式的右邊. 變成了
Y=b0+b1*X1+b2*X2+...+bP*XP+E
這個E是隨機誤差的意思, 條件鬆一點來說, 我們要求 E 的平均數是0就好了, 而標準教科書通常會假設E會服從常態分配!!
舉個最簡單例子: 身高能夠預測體重嗎?
通常, 身高較高的人體重較重, 可是總有人是天生竹竿身材,
因此, 這個隨機誤差就是要用來描述 虛胖/結實/苗條/過瘦 情況, 也就是:
就算一樣是175公分的人(X=175.0), 體重不一定會相同(可能是y=80.0公斤, 或者 y=70.0公斤)
用個虛擬的數據化個圖來看看,
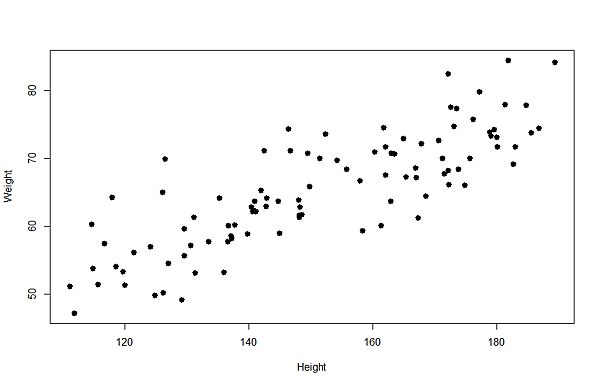
可以看到, 身高越高, 體重會緩緩上升, 而整體趨勢就是用最小平方法求出來的估計的迴歸線:
Weight=16.9588+0.3195*Height
也就是我們可以用這條估計出來的迴歸線, 猜測身高170公分的人的體重.
16.9588+0.3195*170=71.2738
大概是71公斤!!!
※※※線性迴歸分析應注意事項※※※
在進行線性迴歸分析前, 要注意一些事:
1.反應變數是連續型變數嗎? 如果不是連續型變數, 而是Binary data, 上面介紹的迴歸分析是不恰當的
這一個問題就延伸出 邏輯斯迴歸分析.
2.通常會假設反應變數是服從常態分配, 不過有分析過實際資料的人都知道, 數據怎麼可能是常態麻
雖然這個假設在估計迴歸係數值不需要, 但在做統計推論時就非常重要.
3.有發現我們關心的變數間是如何被連結起來嗎?
我們直接假設體重是身高的直線函數,
Weight=b0+b1*Height+E
也就是我們將身高與體重的關係「直接」連結起來了!
然而, 在現實生活中不可能有這麼簡單的事發生.
※※※邏輯斯迴歸分析的概念※※※
現在換個問題:
有什麼條件的車主會額外加買保險?
這問題點典型的商業智慧分析應用. 保險公司希望提高客戶投保率, 不希望亂槍打鳥的讓業務員去拜訪客戶,
將時間浪費在投保意願低的客戶身上.
這時候一樣會去收集數據, 會有反應變數Y與預測變數{X1,...,XP}
不過, 想解決的問題是「會不會加買保險?」, 所以收集的Y最直接就是 買/不買 兩種.
在統計上, 習慣用數字來表示這兩種購買行為. 1表示 會購買保險, 0表示 不會購買保險.
然後預測變數可能就是 性別/職業/薪水/已購買壽險數量...等等.
線姓迴歸有辦法處理這樣的問題嗎?
假設現在收集的預測變數是已購買的壽險數(有投保觀念的人或許比較有可能額外加保車險).
在線性迴歸的表示是:
加保車險=b0+b1*已購買的壽險數+E
散布圖是

可以看到, 購買不同壽險張數的客戶都有加保的意願
然而我們是無法從這張圖看到到底是壽險買多比較有意願加保, 還是買少的加保意願強?
如果還是估計線性迴歸的參數就變成:
是否加保=0.057840+0.025833*已購買的壽險數
現在有個新客戶已知他有購買壽險保單2張, 那你要不花點時間推銷他加保車險?
應用估計出來的迴歸式:
0.057840+0.025833*2=0.1095
這.....0.1095我怎麼知道他是買不買啊?
這個就是線性迴歸應用在二元反應變數的問題之一: 預測值不在合理的解釋範圍/空間中
換個角度想, 我們可以用列連表來看一下購買比例如何
NLI
Purchase 0 1 2 3 4
No 94.12% 95.38% 90.00% 81.82% 62.50%
Yes 5.88% 4.62% 10.00% 18.18% 37.50%
上表的每一行總和都是100%, 因為我的計算方式是: 在相同已購買保單數下, 是否加保車險的比例.
顯然, 加保的比例隨著原本已購買壽險的張數提高(從5.88%到最後的37.5%), 看來真的是有投保觀念的人買車容易再加保啊!!!
這時, 統計學家就想到, 那為什麼我們不轉個彎, 換不同的方向問問題呢?
「已購買壽險數量是不是會影響加保車險的機率?」
所以目標變成:
加保機率=f(已購買壽險數量)
如果要像線性迴歸模型一樣有合理的統計模型, 首先要考慮的兩件事就是
●f這個數值可能範圍只能在0到1之間, 因為機率值最大就是100%, 最小就是0%.
●模仿線性迴歸模型, 我們希望b0+b1*X1+b2*X2+...+bP*XP的取值是從負無窮到正無窮.
如此一來, 在做數值分析求估計值時, 不收斂問題會少一點.
為了要做到這兩件事, 不失一般性, 考慮b0+b1*X1就好!!
因為,
負無窮 < b0+b1*X1 < 正無窮 隱含 負無窮 < -(b0+b1*X1) < 正無窮
所以,
0 < exp[-(b0+b1*X1)] < 正無窮, 其中的exp()是自然指數的意思.
再來, 全部加1
1 < 1+exp[-(b0+b1*X1)] < 正無窮
最後, 取倒數
0 < exp(b0+b1*X1)/[1+exp(b0+b1*X1)] < 1
這樣就滿足上面兩條件,
所以, 我們就直接把會加保車險的機率P(X)連結成
P(X1)= exp(b0+b1*X1)/[1+exp(b0+b1*X1)]
其實,上面的等號右邊是個邏輯斯函數(Logistic function)
所以, 我們可以合理化問題轉成邏輯斯迴歸:
加保機率=exp(b0+b1*已購買壽險數量)/[1+exp(b0+b1*已購買壽險數量)]
而b0跟b1可以用概似函數估算出來, 估計後帶入上式就可以估計會加保車險的機率.
在實際應用上面, 我們可以反求具有什麼特點的客戶會有夠高機會加保車險.
如此, 就可以提高販售出保險的比例, 不用亂槍打鳥, 白做工.
※※※邏輯斯迴歸分析的R程式碼※※※
延續上面的例子, 我們進入正式數據分析
#載入ISLR資料庫, 我們需要的資料在這資料庫裏面
library(ISLR)
#看一下"Caravan",大型敞篷車投保資料集,的樣本數有多少?(5822),收集的變數有幾個?(86)
dim(Caravan)
#可以看一下收集的86個變數名稱. 注意到最後一個是反應變數Purchase
names(Caravan)
#我們選擇其中的ALEVEN變數, 這一個是「購買壽險的數量」, 其中第775筆是購買八張保單的客戶
#因為在5822中只有一個買8張保單的客戶, 其餘客戶購買數皆不超過4張, 所以我們先不考慮該客戶
attach(Caravan)
ALEVEN<-ALEVEN[-775]
YN<-as.numeric(Purchase[-775])-1
#使用R中的glm函數估計邏輯迴歸函數, 記得在family指定binomial
fit<-summary(glm(YN~ALEVEN,family=binomial))
fit
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.78810 0.05711 -48.821 < 2e-16 ***
ALEVEN 0.33485 0.11340 2.953 0.00315 **
所以估計的邏輯斯迴歸是
加保機率=exp(-2.788+0.3349*已購買壽險數量)/[1+exp(-2.788+0.3349*已購買壽險數量)]
如果求加保機率要超過1成才優先考慮為高機率加保潛在客戶, 那我們就可以反求
exp(-2.788+0.3349*已購買壽險數量)/[1+exp(-2.788+0.3349*已購買壽險數量)] > 0.1
==>已購買壽險數量 > [log(0.1/0.9)+2.788]/0.3349 = 1.76
我們發現, 如果購買壽險保單達2張, 那該客戶就有高達1成以上機率會加購車險,
所以, 具有已購買兩張或以上的壽險客戶是優先推銷加保車險客戶!!!
※※※邏輯斯迴歸分析的R程式碼與機器學習※※※
與KNN使用相同資料, 所以以下某些陳述也與KNN演算法相同, 對KNN演算法有興趣讀者請自行連結過去
#載入ISLR資料庫, 我們需要的資料在這資料庫裏面
library(ISLR)
#看一下"Caravan",大型敞篷車投保資料集,的樣本數有多少?(5822),收集的變數有幾個?(86)
dim(Caravan)
#可以看一下收集的86個變數名稱. 注意到最後一個是反應變數Purchase
names(Caravan)
#先看一下變數的敘述統計量
summary(Caravan)
#計算會購買保險的比例是多少?(5.977%)
table(Caravan$Purchase)/dim(Caravan)[1]
使用訓練與測試82法則, 則取訓練筆數:測試筆數=4650:1172
#進行資料整理與分割
Purchase.01<-as.numeric(Caravan[,"Purchase"])-1
train.index<-1:4650
train.X<-Caravan[train.index,-86]
train.Y<-Purchase.01[train.index]
test.X<-Caravan[-train.index,-86]
test.Y<-Purchase.01[-train.index]
train.D<-data.frame(train.X,train.Y)
#進行邏輯斯迴歸估計
logistic<-glm(train.Y~.,data=train.D,family=binomial)
summary(logistic)
#將測試集的預測機率估計出來
pred<-predict(logistic,newdata=test.X,type="response")
pred[1:10]
#設定會加保車險的機率超過10%就是潛在會加保的客戶,把這些人識別出來
Index<-which(pred>=0.1)
predict.01<-rep(0,length(test.Y))
predict.01[Index]<-1
#建立混淆矩陣
Confusion.matrix<-table(Truth=test.Y,Prediction=predict.01)
#我們真正關心的是, 在我們預測會加保的客戶中, 實際上真的有購買的比例是多少? 答案是18.37%
Confusion.matrix[2,2]/sum(Confusion.matrix[,2])
#我們可以試著找找看, 預測的機率值超過多少當作值得拜訪客戶的門檻值?
#最後, 發現只要新進客戶的預測加保機率估計值超過5%就值得去推銷拜訪
Pro<-seq(0.01,0.9,0.01)
Success.Rate<-numeric(length(Pro))
for(i in 1:length(Pro))
{
Index<-which(pred>=Pro[i])
predict.01<-rep(0,length(test.Y))
predict.01[Index]<-1
Confusion.matrix<-table(Truth=test.Y,Prediction=predict.01)
Success.Rate[i]<-Confusion.matrix[2,2]/sum(Confusion.matrix[,2])
print(c(i,Success.Rate[i]))
}
Pro[min(which(Success.Rate>=0.05977*2))]
#以圖形展現不同門檻值對預測成功率的變化
plot(Pro,Success.Rate,pch=19,lwd=3,ylab="針對測試集的成功預測機率值",xlab="值得拜訪的機率門檻值")
lines(Pro,Success.Rate,lwd=1,lty=2,col=4)
abline(h=0.05977,col=2)
abline(h=0.05977*2,col=2,lwd=2,lty=2)
text(0.2,0.07,"隨機拜訪成功率5.977%")
text(0.2,0.13,"比隨機拜訪成功率多2倍,11.954%")
abline(v=0.05,col=6,lwd=2,lty=2)



 留言列表
留言列表


