簡述今天朋友問我的問題:
一到一百中的每一個數,被取中的機會皆相等, 現在每次取樣3個, 取出放回
連續抽取50組. 請問樣本平均數會遵循中央極限定理嗎?
我們先來複習一下,
什麼是中央極限定理(Central Limit Theory)? 大陸稱為趨中定理, 就是
不管母體是什麼分配,只要母體的均值與變異數存在,
只要樣本數夠大, 樣本平均數的抽樣分配會近似常態分配.
顯然,離散型均勻分配的均數與標準差是存在的. 所以上面紅字第一航描述的條件是滿足的.
問題出在"樣本數"夠大, 這一個樣本數夠大紙的是什麼意思?
這一個問題很顯然就是在考這觀念.
根據我十多年的輔導經驗, 八成的人都會誤解成:
只要我重複取樣的組數夠大(這問題的組數就是50),
那畫出來的直方圖就會跟常態分配相近.
可惜, 正解是要看每次用來計算樣本平均數的數據有幾筆, 這裡是取3筆.
所以這一題, 我給的回覆是:
因抽樣數太少,只有3個,
所以要用中央極限定理來說明樣本均值的表現會近似常態,會不如預期的好.
所以我自己花了點時間用R語言寫了個小程式,目的是使用Shapiro-Wilk test檢驗,每次抽取3筆數據
取出放回,共50組, 這50組能通過常態性檢驗嗎? 程式如下:
check.CLT.DUnif<-function(n,N,M=10000,UB=100,LB=1,alpha=0.05)
{
X.mean<-numeric(N)
P.value<-numeric(M)
j<-0
while(TRUE)
{
j<-j+1
set.seed(j)
for(i in 1:N)
{
X<-sample(x=LB:UB,size=n,replace=TRUE)
X.mean[i]<-mean(X)
}
P.value[j]<-shapiro.test(X.mean)$p
if(j==M) break
}
mean(P.value<=alpha)
}
依據上面的R函數, 我來算一下, 每次取樣3個(n), 50個成一組, 使用正態性檢驗,
Level Alpha 設定為5%, 總共模擬10000次.
根據理論, 若資料室從常態母體取樣, 那麼模擬的level Alpha 應該要與名目(Nominal Alpha)相近,也就是數值應該是5%
check.CLT.DUnif(n=3,N=50)
結果是0.0345, 離得有點遠!!
0.0345的意思不就是低估了顯著水準嗎? 雖然還是滿足Level Alpha的定義, 但顯然保守了!
也就是說, 取樣數只有3個,重複取50次, 正態性檢定容易宣稱數據是正態的.
相對來說, 信賴區間也會比較寬, 同樣是95%信心區間, 但較無效率.
那將樣本數分別提升為10與30呢? 我們看結果
check.CLT.DUnif(n=10,N=50)
結果是0.0427
check.CLT.DUnif(n=30,N=50)
結果是0.0466
隨著樣本數增大(3-->10-->30)
如我們所預期的,估計的Alpha Risk 越來越接近目水準
那如果樣本數增大為100呢? 這總應該很滿足中央極限定理的條件了吧! 我們來看
check.CLT.DUnif(n=100,N=50)
答案是0.0508!!! 相當漂亮的估計數值.
這就是我所謂樣本數太少, 會不如預期的意思.
那變動50組這一個數字,但還是固定取樣3個呢? 結果會是什麼? 我們來看看
> check.CLT.DUnif(n=3,N=10)
[1] 0.0411
> check.CLT.DUnif(n=3,N=20)
[1] 0.0363
> check.CLT.DUnif(n=3,N=30)
[1] 0.0359
> check.CLT.DUnif(n=3,N=40)
[1] 0.0369
> check.CLT.DUnif(n=3,N=50)
[1] 0.0345
> check.CLT.DUnif(n=3,N=100)
[1] 0.0396
> check.CLT.DUnif(n=3,N=200)
[1] 0.0775
> check.CLT.DUnif(n=3,N=300)
[1] 0.1279
> check.CLT.DUnif(n=3,N=400)
[1] 0.2026
> check.CLT.DUnif(n=3,N=500)
[1] 0.2943
你看看, 居然發生 隨組數增多 估計的顯著水準往上飆升, 這不就是跟我們說: 中央極限定理不能用啊!!!
因為顯著水準已經不受控了
為什麼? 因為估計的顯著水準越大, 不就表示越容易拒絕H0嗎?
越容易拒絕H0:數據是服從常態分配, 就表示容易相信Ha:數據不是常態分配
因此, 這一個估計的顯著水準, 其實根本變成估計Power了!!
(Note that Power的定義是Ha為真,會拒絕H0的機率.)
其實這樣的解果是蠻合理的, 因為組數越多,更能看出樣本平均值分布的全貌
所以越多證據點出, 不能用中央極限定理啊.
那變動50組這一個數字,但是固定取樣30個呢? 結果會是什麼? 我們來看看
> check.CLT.DUnif(n=30,N=10)
[1] 0.0486
> check.CLT.DUnif(n=30,N=20)
[1] 0.0436
> check.CLT.DUnif(n=30,N=30)
[1] 0.0444
> check.CLT.DUnif(n=30,N=40)
[1] 0.0488
> check.CLT.DUnif(n=30,N=50)
[1] 0.0466
> check.CLT.DUnif(n=30,N=100)
[1] 0.0462
> check.CLT.DUnif(n=30,N=200)
[1] 0.0451
> check.CLT.DUnif(n=30,N=300)
[1] 0.0435
> check.CLT.DUnif(n=30,N=400)
[1] 0.0458
> check.CLT.DUnif(n=30,N=500)
[1] 0.0474
看到沒有, 真金是不怕火煉的
只要是樣本數夠大, 前提符合, 中央極限定理是可以掛保證的
不管你樣本資訊多少, 估計的顯著水準都會維持在0.05附近.
這就是中央極限定理的威力啊!
最後放一張圖來做結束
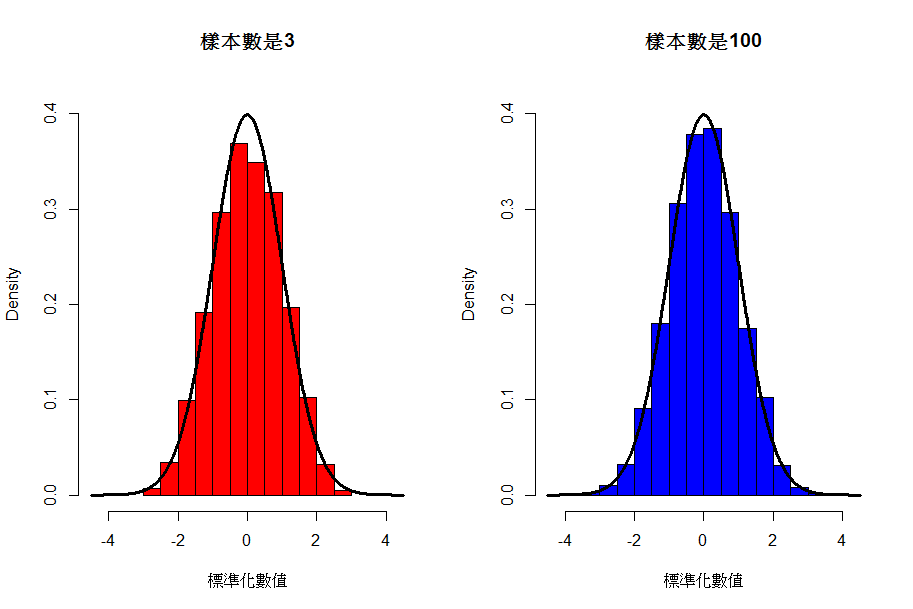
圖中黑色曲線是標準常態分配的機率密度函數,所以為了比較,我也將模擬的數值標準化後繪在同一張圖上
紅色與藍色似乎很相近, 可是關鍵是紅色圖形中的數值分布,幾乎沒有小於-3與大於3的, 光這一點就不滿足常態分配的條件了, 所以這圖的常態性檢定P值是接近0,
而藍色的圖因為樣本數夠大,所以常態性檢定P值是0.6565.
請您好好觀察這兩個數值的不同吧!
那就先介紹到這邊吧!
歡迎留言~~~


 留言列表
留言列表


